Controller technologies used
Various control technologies are used in the process industry to meet the diverse requirements and challenges. Simple processes with stable and linear characteristics can often be efficiently controlled using classic control technologies such as PID controllers. These are particularly suitable for applications where fast and precise reactions are required.
Complex and non-linear processes, on the other hand, require more advanced control technologies such as fuzzy logic controllers or neural networks. These technologies are better able to deal with complex relationships and changes in the course of the process. For processes with slow dynamics and multiple input and output variables, Model Predictive Control (MPC) offers an efficient solution as it can predict and optimize future states.
The choice of suitable control technology also depends on the availability of process data, safety requirements and available resources. Adaptive controls, for example, are suitable for processes whose characteristics change over time, while predictive algorithms can help to optimize energy efficiency and production quality. Ultimately, a combination of different technologies is often used to achieve the best possible results.
Would you like to find out more? Should we call you or would you like to receive further information by e-mail?
I am happy to be there for you!
Sebastian Sturm is your expert when it comes to controller technologies!
Controller technologies
Model predictive control uses a mathematical model of the controlled process to optimally control the controlled variable. For this purpose, the model is continuously compared with the real process variables and used to predict the future behaviour of the process.
We further use this prediction in a real-time optimisation to find the optimal manipulated variable for the current time step. As a result, very fast, stable control of your process is possible, through which we achieve significant improvements (e.g. compared to PID-based concepts).
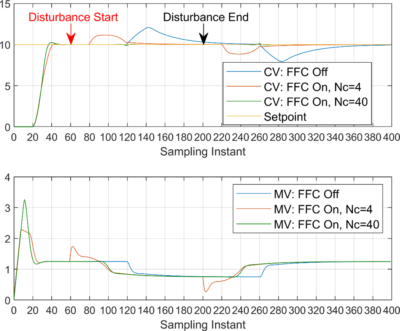 By taking known disturbances into account in the target function, it is possible to compensate for disturbances with very long dead times without critical controlled variable deviation by means of appropriate feedforward control (FFC).
By taking known disturbances into account in the target function, it is possible to compensate for disturbances with very long dead times without critical controlled variable deviation by means of appropriate feedforward control (FFC).
The use of MPC offers significant advantages in the control of non-linear systems. These include, among others, the implicit treatment of manipulated variable constraints as well as the possibility to optimally operate systems very close to these constraints, the simple extension to multivariable systems as well as the model-based consideration of system dead times.
Especially the control of the latter system class represents a typical application of model predictive control structures.
Model Predictive Control (MPC):
-
Uses a dynamic model of the process to predict future states and develop optimal control strategies
-
Particularly suitable for systems with slow dynamics and multiple input and output variables
-
Used in the oil and gas industry, the petrochemical industry and the food industry
Your advantages of MPC control at a glance
-
Control of multi-measurement systems (MIMO) with an MPC
-
Integrate disturbances model, minimise control error
-
Consideration of non-linearities
-
Reacting to known future setpoint changes
-
Direct compensation of dead times
-
Direct consideration of static/dynamic constraints
-
Optimise the process at each time step
-
Accelerate transient process changes
-
Minimise losses due to setpoint changes
-
Enable stability verification
In contrast to classical models, neural networks represent numerous non-linear functions and thus represent complex and multi-dimensional problems.
Any number of complex non-linear effects can be represented, with the major limitation that many process data must be available and the model is only valid for plant states present in these process data (no extrapolability).
Neural networks independently extract relevant correlations from large amounts of data. This makes them a valuable addition to physical-logical modelling, which is often insufficient or only feasible with a great deal of effort.
They use artificial intelligence to model and control complex processes and have the ability to recognize and adapt to non-linear relationships in the process. They are used in pattern recognition and predictive maintenance.
In practice, we use neural networks as so-called black-box models.
We address the following problems with neural networks
-
Non-linear system identification
-
State observer design
-
Controller design
-
Neural adaptive control
-
Neural optimal control
-
Reinforcement learning
-
NLq stability theory
-
PID controller (proportional-integral-derivative controller):
-
Widely used and versatile
-
Consists of three components: the proportional, the integral and the differential part
-
Used to control processes where fast and precise reactions are required
PID controllers are the most versatile type of controller. We adapt the controller behaviour to your specific application through a variety of practical approaches:
-
Intelligent min/max limits
-
Situational freezing of the controller output
-
Feedforward control
-
Gain scheduling for different controller dynamics
-
Anti-windup for cascade controls
-
Limiting controllers that are switched through to the controller output by a min/max selection
-
Controller tracking when the controller is inactive for skip-free switching
Fuzzy logic controller:
-
Uses fuzzy logic to control complex and non-linear systems
-
Particularly useful when mathematical modeling of the system is difficult
-
Frequently used in the chemical industry and in the control of combustion processes
In order to achieve optimal control performance and generate long-term added value, we also incorporate concepts from the field of fuzzy control in the sense of holistic APC solutions into the respective specific customer solutions, depending on the problem and objective.
Adaptive control
-
continuously adjusts the control parameters to take account of changes in system behavior
-
is suitable for processes in which the properties change over time
-
is used in the automotive industry and in the control of bioprocesses
These control technologies are selected and adapted according to the specific requirements and challenges of the respective process. The combination of several technologies can also lead to optimal results.